Speed Time And Distance Worksheet
Speed Distance Time
Speed is a measure of how quickly something moves, so information technology is calculated by dividing distance past fourth dimension .
Make sure y'all are happy with the post-obit topics before continuing.
- Rearranging Formulae
- Units and Conversions
Level 4-v GCSE KS3 



Speed Distance Time – Formula
Speed , distance and fourth dimension are all related by the formula,
s = \dfrac{d}{t}
where due south is speed , d is distance , and t is time . You can rearrange this formula to find the other two, for instance, if we multiply both sides by t and divide both sides by due south, nosotros get,
t = \dfrac{d}{s}
So, we tin calculate the fourth dimension by dividing the distance by the speed .
Typically, nosotros measure altitude in metres (yard), kilometres (km), or miles, and we measure fourth dimension in seconds (s), minutes (mins) or hours (h). As a consequence, the units nosotros use to measure speed are compound units eastward.g m/s or km/h.
Level 1-iii GCSE KS3 



Speed Altitude Fourth dimension – Formula Triangle
A handy mode of remembering how to summate one of speed , distance and fourth dimension is to employ one of the triangles below.
The horizontal line means divide and the \times symbol means multiply.
Nosotros then comprehend up the one we want to observe (represented by a red circle) and complete the calculation using the other two values from the triangle.

s = \dfrac{d}{t} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, d = s \times t \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, t = \dfrac{d}{s}
Level 1-3 GCSE KS3 



Example one: Calculating Speed
A truck travels 110 miles in 2 hours. What is the average speed of the truck?
[2 marks]
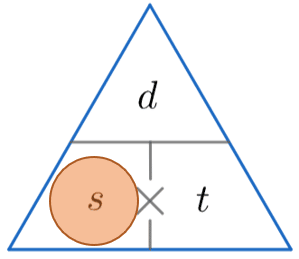

We're looking for speed, then constructing the triangle and covering up the southward, we find nosotros must divide the distance past the time . So
\text{Speed } = 110 \div ii = 55 mph
Level 1-3 GCSE KS3 



Example 2: Calculating Distance
Jesse throws a ball that moves at an average speed of 35 metres per second and travels for a total of 4.5 seconds. Work out the distance travelled by the brawl.
[2 marks]
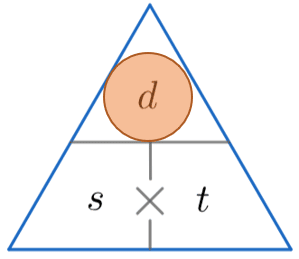

We're looking for distance , so roofing up d, nosotros must multiply the speed by the time. Then
\text{Distance }=35 \times four.five=157.five one thousand
Level 1-three GCSE KS3 



Example 3: Calculating Time
A machine travels at an average speed of 50 mph. How long will it take for the motorcar to travel 12.v miles? Give your answer in minutes.
[ii marks]


We're looking for fourth dimension , so roofing t, we notice we must divide the distance by the speed . And so
\text{Fourth dimension } = \dfrac{12.5}{50} = 0.25 hours
0.25 hours needs to be converted into minutes by multiplying past 60,
\text{Fourth dimension }=0.25\times sixty=15 minutes
Level 1-iii GCSE KS3 



Case Questions

We are calculating the fourth dimension taken, so by roofing upwards the t we can see from the triangle to a higher place that we have to split up distance, d, by speed, southward.
Therefore:
\text{Fourth dimension }=\dfrac{d}{southward}=\dfrac{100}{8.5}=xi.76 s (ii dp).

Nosotros are calculating speed, and so by covering upwardly the s we can meet from the triangle higher up that we take to divide distance, d, by time, t.
However, before we practice that, we accept to ensure that the units match. The speed limit is in 'miles per hour', but the time we take been given is in 'minutes'. This is easy, as 30 minutes is half an hour, or 0.five hours. So, Gustavo'due south boilerplate speed can exist calculated as follows:
\text{speed }=\dfrac{d}{t}=\dfrac{36}{0.5}=72 mph
So, yes, Gustavo is exceeding the speed limit.
In order to calculate the full altitude travelled, we need to rearrange the speed / distance / time formula.
Since
\text{ speed} = \text{ distance} \div \text{ fourth dimension}
then
\text{ distance} = \text{ speed} \times \text{ time}
The distance of the starting time part of the journey tin be calculated as follows:
\text{Distance } = 3 hours \times \, 55 mph = 165 miles
For the 2d role of the journeying, we need to convert the units so that they match. The speed has been given in miles per hour whereas the time has been given in minutes. We can either convert the minutes into hours or we can catechumen the speed class miles per hour to miles per minute. Converting minutes to hours is probably the easier choice:
90 minutes = 1\frac{one}{2} hours or 1.5 hours
The altitude of the second part of the journeying can be calculated as follows:
\text{Distance } = one.5 hours \times \, 48 mph = 72 miles
Therefore the full distance travelled is
165 + 72 = 237 miles
Nosotros know that to calculate speed, we need to carve up altitude by time equally per the formula:
\text{ speed} = \text{ distance} \div \text{ time}
The only issue we have in this question is that the distance has been written as '210 meg', which is not that helpful every bit 'million' has been written as a word and not in figures. The first thing we will need to practice is convert 210 million into figures, hopefully remembering that a 1000000 has 6 zeros:
210 meg = 210,000,000
The time taken has been expressed in minutes and seconds which causes an boosted problem. Nosotros accept been asked to give an reply in kilometres per 2d, so we demand to convert the time from minutes and seconds to seconds.
11 minutes = xi \times lx seconds = 660 seconds
11 minutes and 40 seconds = 660 seconds + \, 40 seconds = 700 seconds
Nosotros are now in a position to summate the speed of light as follows:
\text{ Speed of light} = 210,000,000 km \div \, 700 seconds = 300,000 km/southward
We know that to calculate altitude, we demand to multiply speed past time as per the formula:
\text{ speed} = \text{ distance} \div \text{ time}
Hence converting 35 years to seconds:
35 years =35\times365\times24\times60\times60=1.104\times10^9 seconds
The calculation becomes:
\text{ altitude} = 17 \times (one.104\times10^9) =1.88\times10^{ten} km
Related Topics
Worksheet and Instance Questions
Drill Questions
Speed Time And Distance Worksheet,
Source: https://mmerevise.co.uk/gcse-maths-revision/speed-distance-time-gcse-revision-and-worksheets/
Posted by: mirandacoulp1949.blogspot.com


0 Response to "Speed Time And Distance Worksheet"
Post a Comment